Crédit : Arno Smit sur Unsplash

Vers un réseau profond pour la classification des feuilles d'arbres

Introduction

En novembre dernier, j'avais posté un article qui traitait des réseaux de convolution (essentiellement de la découverte à l'époque). Nous avions étudié un jeu de données restreint (240 images de feuilles d'arbres malades) et construit un modèle de classification (réseau de neurones) qui se reposait sur une couche de convolution. Les résultats n'étaient pas mauvais (presque 80% en validation), mais le réseau n'était pas robuste. En effet, l'augmentation des données (rotations, translations) n'était pas appliquée au moment de l'entraînement et les prédictions du réseau sur des données plus "exotiques" (par exemple, des images issues du jeu de validation auxquelles on a imposé une rotation) étaient mauvaises.

Peut-on obtenir d'aussi bon résultats que précédemment (80% en validation, au moins) avec des images plus réalistes ? C'est ce que nous allons essayer de faire aujourd'hui, en utilisant un réseau plus profond.

Situation

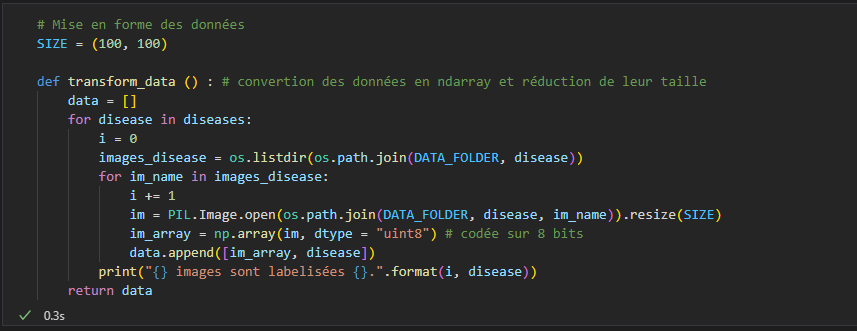
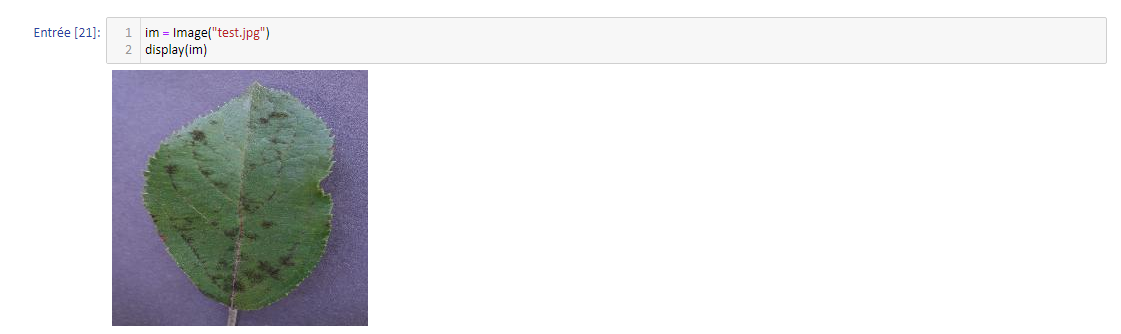
Nous disposons toujours d'environ 240 images de feuilles d'arbres malades (ce qui est peu pour entraîner un réseau profond !). On peut les représenter grâce à Python (nous utiliserons Jupyter Notebook) :

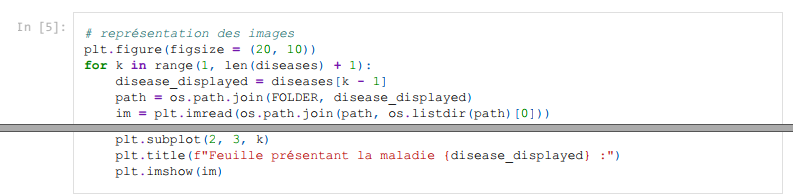
Les images s'affichent ainsi :

Les courbes typiques d'entraînement du modèle précédent (1 couche de convolution 2D à l'entrée, 1 couche de Pooling2D, 1 couche de Flatten pour repasser sur une partie dense et 2 couches Dense pour obtenir le vecteur de classification à 5 composantes) étaient de la forme (avec Data Augmentation appliquée !) :

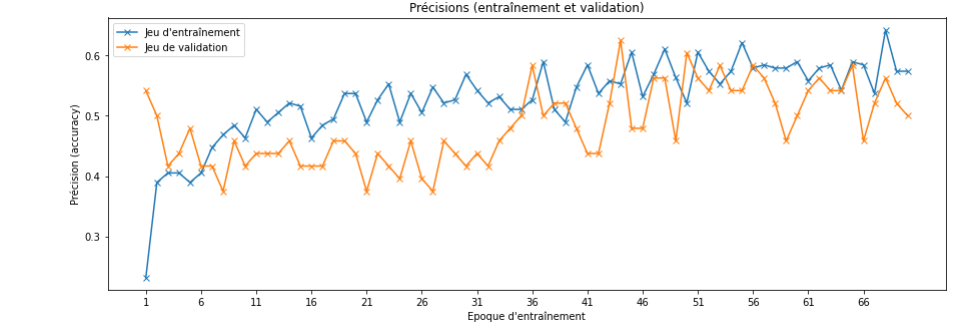
On observe donc une précision sur le jeu d'entraînement de 55% environ (50% en validation) : ce n'est pas complétement à jeter étant donné le nombre de classes (5, donc un modèle aléatoire obtiendrait une précision moyenne de 20%) mais c'est normalement améliorable.

Vers un nouveau modèle

On va désormais appliquer une augmentation des données (instance de l'objet ImageDataGenerator disponible dans Keras) :

J'ai fait le choix de ne pas garder les translations d'images (image décalée horizontalement ou verticalement d'une certaine fraction) car les modes de remplissage des "trous" engendrés par la méthode ne me semblent pas pertinents (les pixels à la frontière sont répliqués en mode "nearest"). On obtiendrait des images qui sembleraient avoir "bavé" du côté opposé à la translation. En revanche, on pourrait certainement couper certaines images (car les feuilles sont toujours centrées sur les images) pour s'assurer que le réseau apprend bien des motifs présents sur les feuilles, et pas sur le fond (qui serait alors effacé par la transformation).
Seules les rotations sont gardées (pm. 180° : n'importe quel angle est désormais possible dans le jeu de données). Cette méthode présente le grand avantage d'être sans remplissage (car aucun pixel n'est supprimé !) et assure des tailles d'images constantes (nécessaire pour le réseau).
Le réseau précédent était :

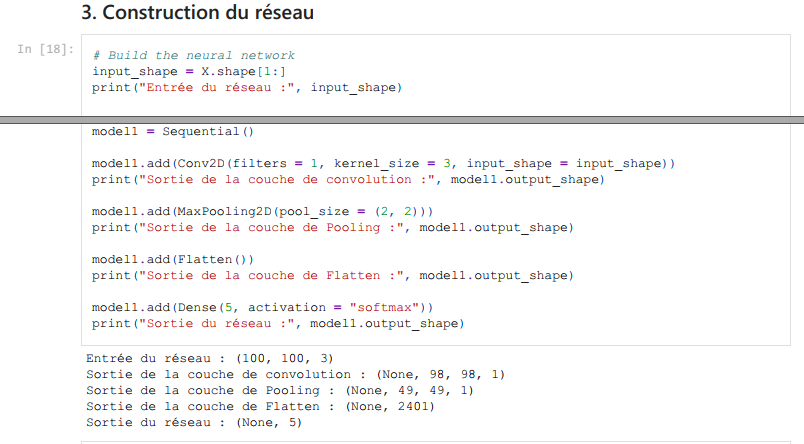
Et nous utilisions la métrique "accuracy" (précision : taux de bonnes classifications) ainsi que la fonction de perte (pour la descente de gradient) "entropie croisée". Elle est définie comme suit :

L'illustration rappelle la nécéssité de joindre une activation softmax (strictement positive) à une telle fonction de perte. La descente de gradient (mise à jour des paramètres du modèle neuronal) se faisait en utilisant l'"optimizer" Adam (qui utilise les gradients passés pour la mise à jour). Sans entrer dans le détail, nous garderons cet "optimizer", ainsi que la même fonction de perte et la même métrique. Le modèle neuronal, en revanche, sera modifié.

On peut, pour savoir comment construire le nouveau réseau, étudier les features maps (résultats intermédiaires) de ce modèle :

Cette ligne définit un modèle intermédiaire composé des sorties des couches succesives du réseau initial : très pratique pour étudier le séquençage des opérations ! On accède aux résultats intermédiaires via cet objet. Les images arrivent dans le réseau codées sur 3 couleurs ("RGB channels") et de taille 100 par 100 (constante définie dans le programme). On regarde le résultat après la 1ère couche (convolution) :

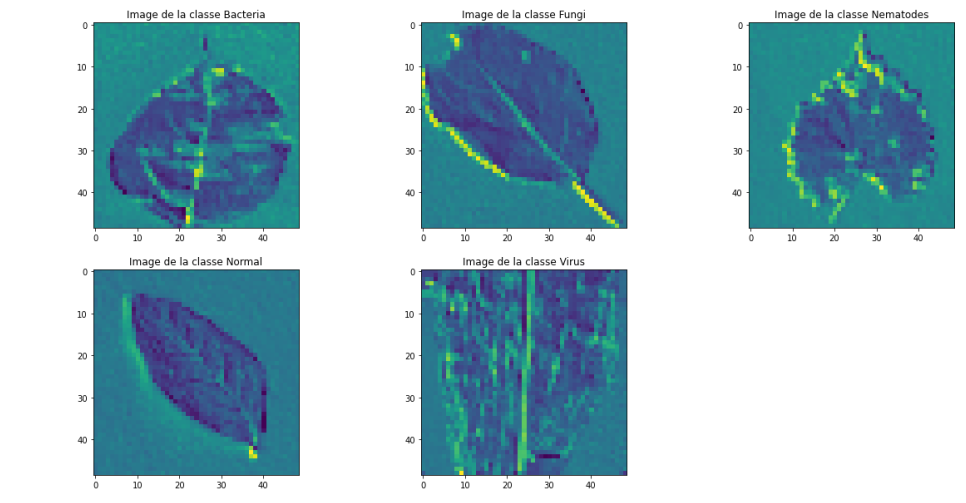
Résultats pour chacune des classes après la 1ère couche de convolution. On repère bien les pixels plus clairs (attention, ils sont standardisés !) sur la classe virus. Les contours sont également bien identifiés mais ne sont pas très utiles, à part à la classification des "Fungi" (la maladie attaque le contour des feuilles). Les zones brunes des "Nematodes" sont bien visibles aussi. Le dégradé causé par les bactéries (classe 1, 1ère image) permettra aussi sans doute d'aider à la classification. On observe bien que le fond (uniforme) n'aide pas du tout au niveau de l'information (et c'est normal). La couche de convolution, bien que simple, apporte déjà beaucoup d'informations sur le traitement des données !
La couche suivant est une couche de Pooling, étudions sa sortie :

Peu d'effet ! Il faudrait ajouter plus de couches de convolution avant pour permettre au réseau de retirer des détails plus fins des images et ne pas mettre de couche de Pooling aussi tôt (plutôt après quelques couches de convolution).

Construction d'un modèle plus profond

On commence, comme d'habitude, par séparé le jeu de données (mélangé au préalable par la fonction numpy.shuffle(), possible ici car les données sont indépendantes) en lots pour l'entraînement et la validation. Note : pas de cross-validation ici, bien que cela devrait être mis en place dans une prochaine version. Etant donné le peu de données disponibles, on pourrait s'intéresser à des schémas de validation de type leave-one-out (validation tournante sur 1 seul individu).

Pour la construction du réseau (enfin !), on utilise l'analyse précédente : plusieurs couches de convolution permettront de tirer des motifs plus complexes des images. Encore une fois, notre principal problème ici est le manque de données, c'est pourquoi aller jusqu'à 3 couches successives de convolutions me paraît peu pertinent (trop de paramètres à entraîner !). Il ne faut pas surcharger le réseau.
Ainsi, on commence le réseau par 2 couches de convolution successives, suivies d'une couche de Pooling. Vient ensuite une couche de Dropout pour éviter l'overfitting et une couche de Flatten pour effectuer la transition vers la partie dense. On ferme le réseau par une couche Dense à 5 composantes et activation "softmax" : le vecteur de probabilité.
La couche de Dropout de paramètre 0.2 (20%) permet de mettre à 0 20% des poids (aléatoirement) entre la couche de Pooling et la couche de Flatten durant l'entraînement (seulement !).

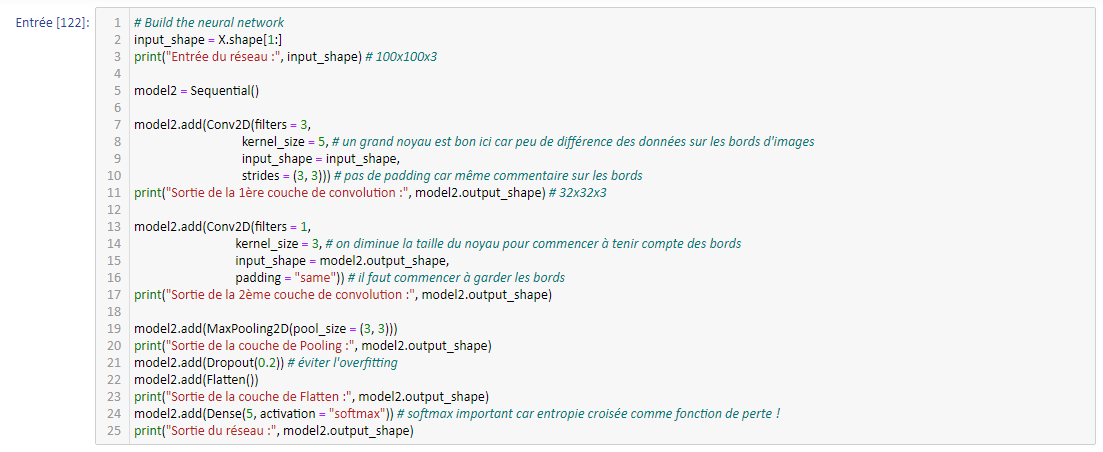
C'est le moment de compiler et d'afficher le résumé du réseau :

La couche Dense finale est complétement connectée à celle précédente (couche Flatten, et indirectement avec les autres car pas de paramètres sur les couches précédentes), ce qui la rend très dense (d'où son nom) en paramètres. On peut d'ailleurs faire le compte nous-mêmes : avec 100 neurones sur la couche de Flatten et 5 sur la couche Dense finale, la matrice de transition contient 500 paramètres, à quoi nous ajoutons un vecteur de biais de taille 5, soit 505 paramètres en tout. Au final, nous obtenons un réseau très (trop) grand par rapport aux données disponibles, mais qui fonctionne bien empiriquement du fait de sa profondeur (surtout grâce aux deux couches de convolution liminaires) :

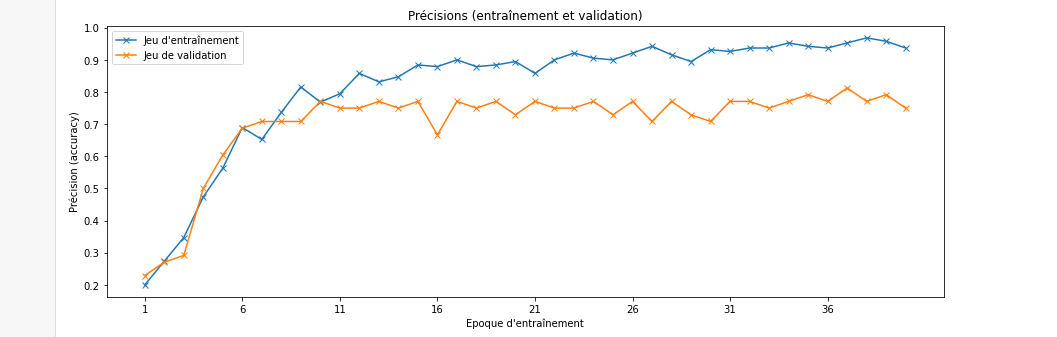
Quasiment 80% de précision sur des données augmentées en validation, c'est sans doute améliorable avec plus de données en entrée (et un travail plus approfondi sur le réseau, pour un prochain article). On peut faire le calcul du ratio paramètres à entraîner/données d'entraînement : 761/190 = 4 ! Une donnée d'entraînement doit fixer 4 paramètres (sans compter sur les époques, qui permettent de gommer ce problème). C'est un compte qui illustre bien la nécessité d'avoir une quantité de données avant de pouvoir construire des modèles profonds.

Crédit : Louise Raoult sur Unsplash

Classification des maladies des feuilles par un réseau de convolution

Introduction

On souhaite dans ce projet étudier certaines maladies affectant les feuilles des plantes et des arbres. Plus particulièrement, on voudrait parvenir, à la donnée d'une feuille quelconque, à déterminer si elle est malade ou pas, et le cas échéant à classifier le type de mal qui l'affecte. C'est un problème de classification multi-classes. En effet, nous allons faire l'hypothèse que chaque feuille est soit saine, soit affectée par une unique maladie. La sortie du modèle de classification sera donc "1 choix parmi N classes".

Pour y arriver, nous allons utiliser un réseau de neurones de type CNN (réseau à convolutions). Les réseaux de neurones sont une classe de modèles qui permettent de faire de la classification mais pas seulement. On peut également faire de la régression ou de la génération de données. Pour schématiser, un réseau de neurones est un embriquement (séquentiel le plus souvent) de sous-modèles linéaires, joints par des fonctions dites d'activation, qui sont non-linéaires. Ce sont ces dernières qui permettent de briser la linéarité du modèle et qui lui permettent d'apprendre une représentation complexe des données d'entrée.

La famille de réseaux de neurones la plus adaptée au traitement d'images est celle des réseaux de convolution (CNN). Pour pouvoir entraîner le modèle a reconnaître les maladies des feuilles, il va nous falloir une base de données contenant des images déjà annotées. Pour chaque image de la base, un label précisera si la feuille est malade ou non, et le cas échéant donnera le nom de la maladie.

La base de données provient du site Kaggle.

Chargement et découverte des données

La liste des librairies nécessaires au projet est disponible au début du notebook (accessible sur mon GitHub).

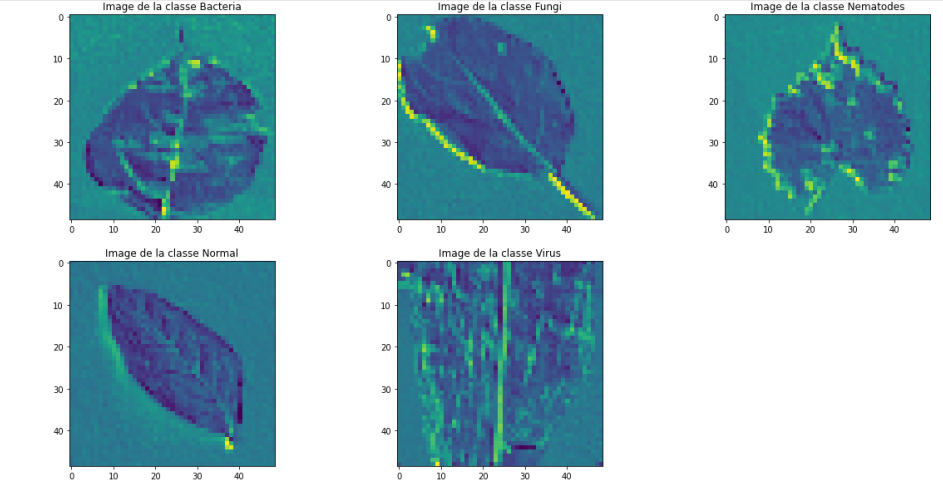
La première chose à faire est d'explorer le jeu de données pour en connaître la composition. On va afficher une image de chaque maladie pour avoir un aperçu visuel de la diversité des classes.

239 images annotées, c'est (très) peu, surtout pour entraîner un modèle d'apprentissage profond. Ce sera l'occasion d'illustrer certaines techniques d'augmentation de données, afin de faire croître ce nombre avant de l'utiliser pour entraîner un petit modèle. Les images montrent des individus appartenant aux 5 classes du problème (dans l'ordre) : feuille saine, feuille attaquée par des nématodes (vers), feuille attaquée par une bactérie, par un virus et enfin par un champignon.

On peut enfin étudier la répartition des images dans chacune des classes :

Le résultat suggère que chacune des classes possèdent environ 50 représentants dans la base de donnée. Avoir des classes équilibrées en nombre d'individus est bénéfique car le modèle aura plus tendance à apprendre de manière parcimonieuse. En effet, à la limite où une classe est sur-représentée (dans l'ensemble d'entraînement et de validation), il suffit au modèle de savoir correctement gérer les exemples de cette classe pour minimiser sa fonction de coût lors de l'entraînement, ce qui n'est pas le but et risque d'induire une forte erreur de généralisation (sur l'ensemble de test).

Préparation des données

Après avoir chargée les données en couples (image, annotation de classe), on va les mélanger pour avoir un ordre d'apparition aléatoire.

On normalise les valeurs RGB des données d'entrée (couleur) en les divisant par 255 (valeur maximale d'un pixel sur 8 bits). Cela permettra d'optimiser la vitesse d'entraînement du modèle (marginalement ici, peut-être intéressant sur de plus gros modèles).
Ensuite, on va vectoriser les labels des données. Les labels sont pour l'instant des entiers (0 pour désigner une feuille saine jusqu'à 4 pour désigner une feuille attaquée par un champignon). La fonction to_categorical de Tensorflow (API Python Keras) permet de convertir les labels en vecteurs à 5 composantes (des 0 partout et un 1 au rang de la bonne classe, pour chaque classe possible parmi les 5). On sera ainsi compatible avec la sortie du réseau de neurones, dont la dernière couche renvoie un vecteur de probabilité de la taille du nombre de classes du problème. Nous le détaillerons plus loin, mais si le modèle possède ce format de sortie, c'est grâce à une activation de type Softmax.

Augmentation des données puis découpage en jeux d'entraînement, de validation et de test

À ce stade, il faut nous demander quelles transformations sont applicables aux données pour augmenter le nombre d'images dans la base d'entraînement, tout en préservant la nature des données. Toutes les opérations ne sont pas permises. Par exemple, si l'on souhaitait construire un modèle de reconnaissance de chiffres manuscrits, effectuer une rotation à 180° des images d'entrées transformerait les 6 en 9, ce qui changerait la signification des données (et l'on souhaite absolument l'éviter car cela induit un coût de ré-annotation, ce qui va à contre-sens de ce que l'on essaie de faire ici).
Les opérations que l'on va effectuer sont les suivantes : Enfin, on utilise un objet permettant d'appliquer des rotations et des translations sur les images de la base de données (l'objet agit directement sur les tableaux 2D) :

Construction du modèle

À ce stade, on peut utiliser la fonction test-train-split de Scikit-Learn avec un ratio de 80% pour séparer les données en jeux d'entraînement et de validation :



Vient alors le temps de construire le réseau de neurones. C'est le coeur de l'algorithme. J'opte pour un réseau très simple (et sans doute sous-optimal) pour découvrir la couche de convolution 2D de tensorflow :



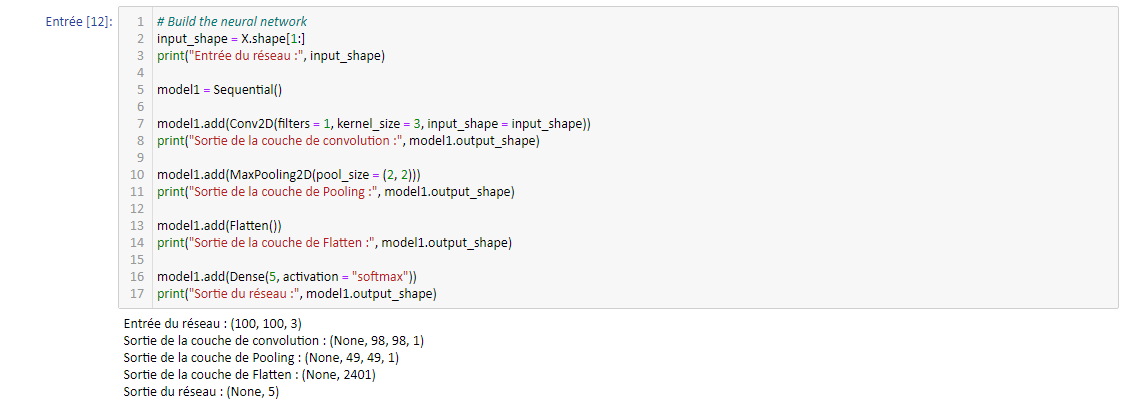
Prenons le temps d'expliquer les couches utilisées.
Les données arrivent au format np.array de taille 100x100x3 dans le réseau (le 3 provient du format RGB des images en couleurs). La 1ère couche est la couche de convolution. Elle va générer un noyau de convolution (ici de taille 3x3x3 car nous sommes en 3 dimensions), un cube numérique que l'on va faire "glisser" le long d'une entrée pour balayer tout le cube de données entrant.
Pour simplifier, supposons des entrées 2D. Le noyau de 3x3 va glisser d'abord de droite à gauche puis de haut en bas sur la matrice de données en entrée. Pour chaque position du noyau de convolution, on multiplie la valeur de la cellule du noyau et celle de la matrice en superposition. En répétant l'opération sur toute la surface couverte par le noyau pour une position donnée et en sommant les multiplications, on obtient la valeur de la convolution pour cette position relative noyau/matrice. Le principe est le même en 3D.

Je prends le batch-size (le nombre d'images que l'on envoie au réseau avant la descente de gradient) à 1 car je n'ai pas beaucoup de données. D'autre part, je choisis de prendre un noyau carré (un seul paramètre entier passé à l'option kernel-size) de taille 3 (en réalité le noyau est cubique car l'image d'entrée est en couleurs, le résultat d'une cellule sera la somme de 3 filtres de convolution, chacun de taille (3, 3) et valables sur un des trois "color-channel"). Enfin, je me limite à un seul filtre (une seule dimension de sortie correspondant à un seul noyau cubique de convolution).
La descente de gradient optimisera le filtre de la couche Conv2D contenant 3*3*3 +1 = 28 paramètres (le +1 correspond au biais et est un scalaire).

La couche suivant est celle de MaxPooling2D. Elle génère un noyau carré de taille 2 (à voir comme une "loupe" qui regarde la matrice d'entrée qui lui arrive en entrée) se déplaçant sans chevauchement sur le résultat de la couche Conv2D (taille (98, 98, 1) du fait de la dimension choisie pour le noyau). Cette "loupe" prend la valeur maximale de chaque zone parcourue : la sortie est donc de taille (49, 49, 1) et, on l'espère, est capable de faire ressortir les contrastes sur l'image (en association avec Conv2D).

On termine le réseau par un couche de remise à plat ("Flatten") qui fait la transformation "données 2D" vers "liste 1D", ainsi qu'une couche Dense de 5 neurones. Cette dernière est liée à la fonction d'activation Softmax afin obtenir un vecteur de probabilité normalisé (sur lequel on calculera la perte par rapport au vrai label à chaque itération).

On termine par compiler le modèle :



On choisit l'entropie croisée comme fonction de perte pour le modèle. Dans notre cas, une seule prédiction de classe est correcte à chaque itération (pas de multi-classes) donc la perte s'écrit simplement comme :


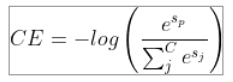
où les Si sont les valeurs en entrée de la couche Dense du réseau pour chacune des classes. Dans notre cas, C = 5 (nombre de classes).
On se donne également une métrique pour suivre l'avancement de l'entraînement : la précision. Elle vaut 1 pour une itération donnée si la classification est correcte, 0 sinon. On s'attend à ce que la précision augmente avec les vagues d'entraînement.
Je ne m'étends pas sur le choix de l'optimiseur Adam car j'attends de mieux comprendre les mathématiques de la descente de gradient stochastique. Passons aux simulations.

Simulation et résultats

On entraîne le réseau avec 5 époques, correspondant au nombre de fois où toutes les données d'entraînement sont données au réseau (on pourrait optimiser ce paramètre par itérations successives) :



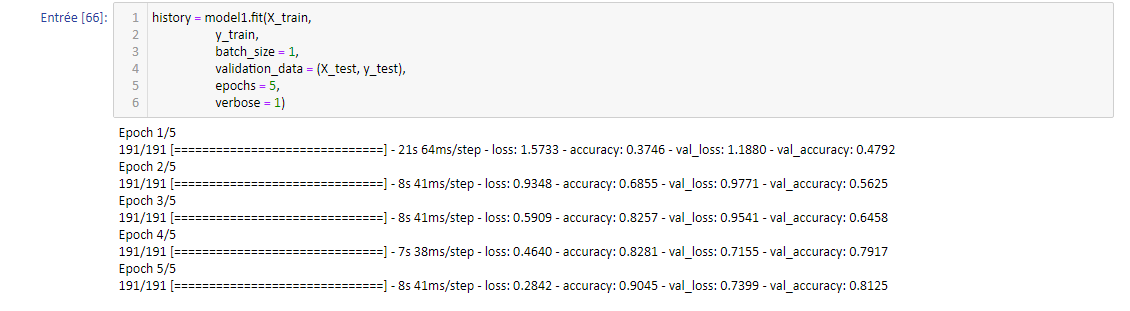
On observe que la précision augmente durant les époques, ce qui est bon signe, jusqu'à atteindre 90% sur le jeu d'entraînement et 81% sur le jeu de validation. C'est un bon score pour un réseau minimaliste comme celui déployé. La courbe obtenue est la suivante :



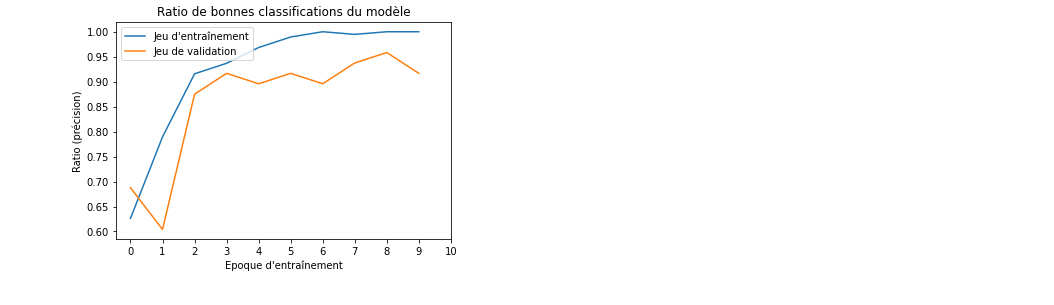
On remarque l'absence d'overfitting (en effet, l'erreur d'entraînement ne repart pas à la hausse avec les époques) et le début d'une stabilisation. On peut, pour terminer, essayer de prédire la maladie d'une image extérieure aux jeux utilisés jusqu'ici :



Le modèle entraîné prédit la classe 1 (c'est-à-dire "Bactérie") à 65% et la classe "Normal" à 35%. L'image représente une feuille faiblement atteinte par une bactérie, donc la classe prédite majoritairement est la bonne. On peut comprendre la confusion en observant les larges zones saines de la feuille. Il faudrait bien entendu tester plusieurs autres données extérieures, mais cela sera pour une prochaine fois ! Nous tenterons alors d'améliorer le modèle simpliste construit ici.

Crédit : darengd sur Unsplash

Algorithme génétique : évolution d'un champ de maïs

Introduction

Nous étudions un champ de maïs. On considère chaque épi de maïs comme un individu indépendant. L'ensemble des épis constitue une population.

Le principe de l'étude est le suivant : on démarre avec une population de N individus (la taille du champ). Nous allons simuler l'évolution du champ dans le temps et suivre son rendement. Le rendement du champ est simplement la somme des rendements individuels des épis qui le constituent. Le rendement effectif d'un épi est exprimé comme une fraction du rendement maximal atteignable par individu (constante commune à tous les épis).

Initialement, les rendements des épis sont distribués au hasard. À chaque tour A (1 tour représente une année), une sélection empirique a lieu. D'abord, on identifie une partie des meilleurs individus (ceux qui ont le meilleur rendement) pour planter de nouveau leurs graines l'année suivante. Ensuite, pour introduire volontairement de la diversité génétique dans le champ, on fait de même avec une partie des individus les moins performants.

À ce stade, nous disposons de N' individus pour peupler le champ l'année A+1 (N' < N). Pour compléter la population, l'idée est alors de croiser les individus retenus afin d'obtenir des épis de maïs hybrides.

Enfin, pour pimenter les choses, on supposera que les épis de maïs peuvent "muter". Le rendement d'un épi peut ainsi varier d'une année à l'autre avec une probabilité p << 1.

Implémentation

4 fonctions principales permettent de réaliser des simulations. D'abord, une fonction individual crée un individu en lui associant un rendement. Ensuite, une fonction population crée le champ de maïs. Il faut également définir une fonction grade permettant d'associer un score au champ pour une année donnée. Enfin, la fonction principale, evolve, permet de construire les générations dans le champ de maïs (elle sera appelée chaque année).

La fonction evolve est séparée en plusieurs parties. D'abord, on sélectionne les individus qui ont été les plus performants lors de l'année qui vient de s'écouler. Ils sont ajoutés aux individus de l'année qui arrive.
Ensuite, on en fait muter certains (sélectionnés aléatoirement). Le nouveau rendement est alors tiré aléatoirement entre deux bornes constantes.
Enfin, les individus retenus (dont ceux mutés) sont croisés pour engendrer de nouveaux épis de maïs. Le rendement d'un épi enfant est tiré uniformément entre les rendements de ses deux parents. On aurait pu choisir d'autres distributions (par exemple, une distribution normale centrée sur le rendement moyen des parents).

Simulations

Pour la simulation, on choisit de prendre des rendements entre 1 et 10 (unité arbitraire) et un champ de 100 par 100 (donc 10.000 épis). On mènera l'étude sur 100 générations et on visualisera le rendement du champ sous la forme d'une carte de chaleur.

La distribution initiale est :
Après 1 sélection :
Après 2 sélections :
Après 10 sélections :
Après 20 sélections :
Observations. La répartition initiale semble effectivement aléatoire, on y osberve des rendements faibles (en blancs et vert clair) et forts (en vert foncé). Le champ est donc initialement "naturel" : aucune sélection n'a encore eu lieu. Après la 1ère sélection, le champ apparaît déjà globalement plus foncé. Son rendement est donc, en moyenne, meilleur. D'une façon générale, le rendement moyen est croissant avec le temps : la sélection fonctionne !

On remarque que, de la figure 1 à la 2, certains épis avec un excellent rendement sont gardés. Voir par exemple le 2ème épi de la 1ère ligne. Cela illustre le principe de sélection des meilleurs individus. Dès la 2ème sélection (tour 3 de l'itération), le champ possède un très bon rendement moyen. Certaines zones blanches demeurent, représentant le principe de diversité génétique (certains individus peu performants sont gardés). Dès le tour 11, un régime permanent semble s'installer. En effet, en comparant le tour 11 au 21ème (après 20 sélections), on s'aperçoit que le champ évolue peu. Localement toutefois, certaines zones spatiales voient leur rendement modifié : cela illustre la partie "mutation" des épis : certaines zones performantes peuvent, d'un tour à l'autre, être déstabilisées par le changement brutal du rendement d'un épi muté.

Ce sont ces mutations qui expliquent que le champ, au fil du temps, ne converge pas vers le champ "parfait" (et que son rendement moyen ne converge pas vers le maximum atteignable, 10 ici).

Un autre effet lié aux mutations entre également en jeu : la mutation ayant lieu après la sélection des parents d'une année A, les épis mutés jouent un grand rôle dans le peuplement de l'année A+1. Ce phénomène explique par exemple en partie les zones de rendement moyen : un des parents est un épi muté et l'autre un individu performant au rendement parfait. Cependant, d'autres explications sont possibles : un individu muté du tour d'avant est gardé par diversité génétique et peut aussi être croisé, ou un individu du tour d'avant a subi une mutation diminuant son rendement d'un haut niveau vers un niveau moyen.

Pour conclure et illustrer ces remarques, on trace l'évolution de l'écart du rendement moyen du champ au rendement idéal (cas où tous les épis ont un rendement de 10) au fil du temps :
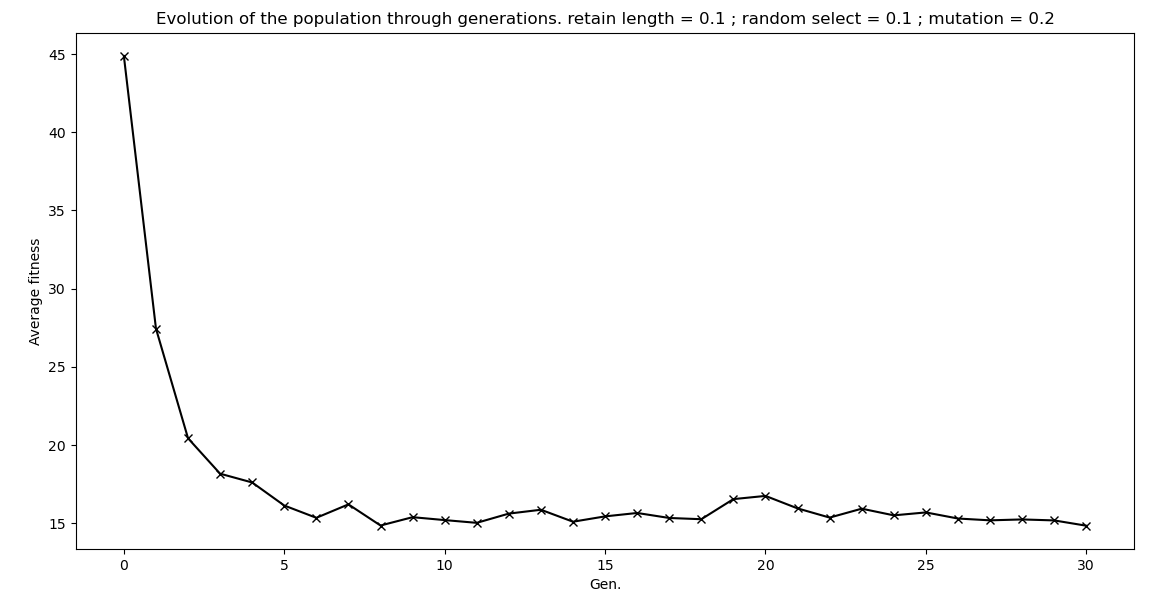
On observe une convergence vers la valeur en régime permanent à partir d'environ 10 générations (ce qui est cohérent avec nos remarques).
On relève également que le champ ne converge pas vers la configuration de rendement idéal (ici, 15% d'écart en régime permanent). Cela est directement en lien avec les remarques ci-dessus à propos des mutations et de la diversité génétique.
Enfin, on lit un écart initial du champ à sa configuration idéale de 45%, ce qui est cohérent avec le fait que le champ soit, à l'origine, peuplé avec des épis de rendement aléatoire entre 1 et 10. En effet, à t = 0, on a un rendement moyen de 5, ce qui représente un écart d'environ 50% au cas idéal, dans lequel tous les épis auraient un rendement maximal.
On pourrait aussi jouer sur les paramètres retain_length, mutate et random_select pour comparer les évolutions des champs, mais cela sera pour un prochain article !

Crédit : Max Ducourneau sur Unsplash

Prédire la taille des poissons par régression : analyse exploratoire des données (1/2)

Introduction

Traditionnellement, le point de départ d'un projet de science des données est la découverte de ces dernières. Des structures de données très pratiques existent, comme par exemple les DataFrames de la librairie Pandas. On peut ainsi obtenir rapidement des premières statistiques empiriques sur les données de travail, et se faire un premier aperçu des traitements à appliquer (par ex. : détection de données manquantes, features avec des distributions asymétriques ou points extrêmes, "outliers").

Aujourd'hui, nous étudierons des données caractérisant des spécimens de poissons sur un marché. Elles ont été publiées sur Kaggle (https://www.kaggle.com/aungpyaeap/fish-market) par Aung Pyae.

Lecture des données, premières statistiques

Nous travaillerons avec les librairies courantes : Pandas, Matplotlib, Numpy.

Après avoir chargé les données avec Pandas, le premier réflexe est souvent d'afficher les premières lignes avec la méthode head du DataFrame :

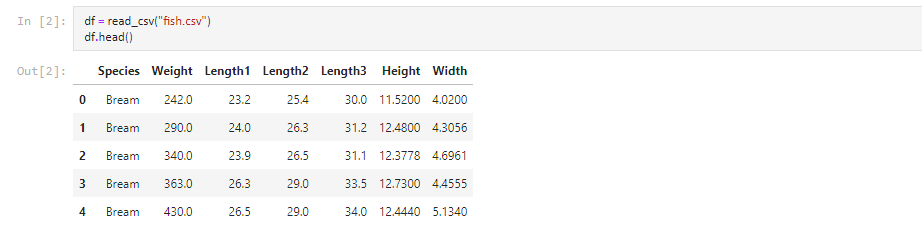
Nous sommes donc en présence d'une variable à expliquer, dite "cible/target" (Weight, la masse), et de 5 variables explicatives (l'espèce, trois longueurs, la hauteur et l'épaisseur), dites "features". À l'exception de l'espèce, toutes sont numériques. On peut regarder les grandeurs statistiques des distributions avec la méthode describe :

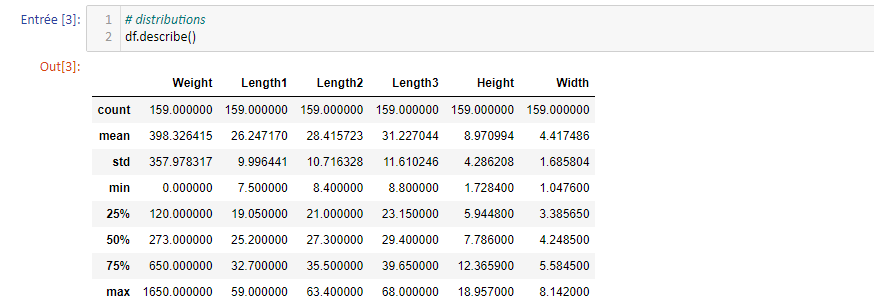
Les moyennes et écart-types peuvent être analysées à la lumière d'une grandeur adimensionnée, plus parlante, le coefficient de variation. Il est défini comme :

Dans l'ordre des colonnes (mis à part la colonne catégorique, espèces), nous obtenons : [0.9, 0.38, 0.38, 0.37, 0.48, 0.38]. La cible possède donc une distribution beaucoup plus éparpillée que les variables explicatives.

On remarque également que la masse s'annule (voir min) : une donnée (au moins) manque donc. Il s'agit de la supprimer. Pour le faire le plus facilement possible, NumPy possède des masques. Le principe est simple : à partir d'une condition booléenne (True/False), une colonne est passée au peigne fin et toutes les lignes (individus) pour lesquelles l'attribut de la colonne ne respecte pas la condition sortent du lot. On peut ensuite passer le masque à la fonction numpy.where qui affiche NaN sur les lignes à supprimer. Il ne reste plus qu'à appliquer une méthode de suppression :

Représentations graphiques

Passons ensuite à la visualisation. C'est une façon rapide et intuitive de repérer les corrélations et liens entre les variables du jeu de données. La première chose à faire est de charger les features dans des variables séparées :

Intéressons-nous à la relation masse/côtes (les côtes sont des prises de mesure caractérisant des poissons : longueur droite, diagonale et section) :
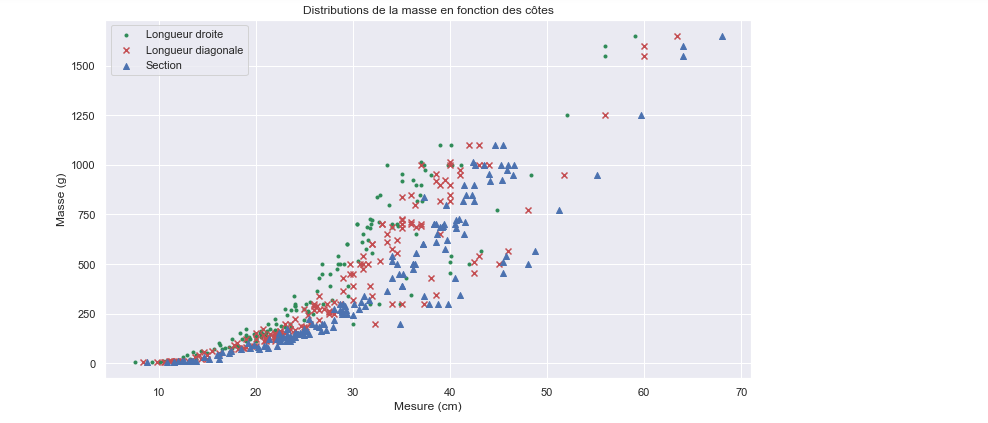L'abcisse correspond à une mesure en cm.
On semble déceler une corrélation entre ces trois features. En effet, la distribution de masse semble suivre la même tendance pour chacune d'elle avec une translation vers les abcisses croissantes. Qu'en est-il pour les autres variables ?

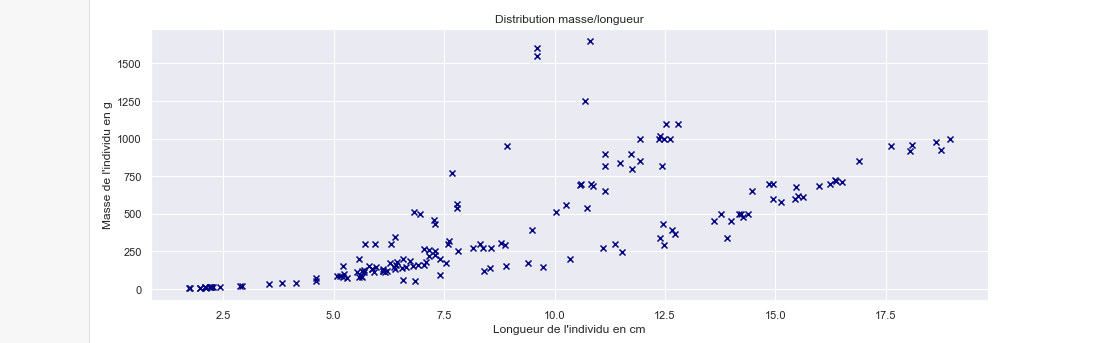
Un modèle polynomial conviendrait sur chacune des trois "branches". On peut se demander d'où viennent ces tendances si bien distinctes. La piste d'espèces différentes est envisageable : une variable catégorique peut souvent expliquer des comportements "définis par blocs" dans les données. Nous allons voir que c'est effectivement le cas ici. Il faut pour cela regarder les distributions marginales selon les espèces. Utilisons encore la fonction scatter de Matplotlib :



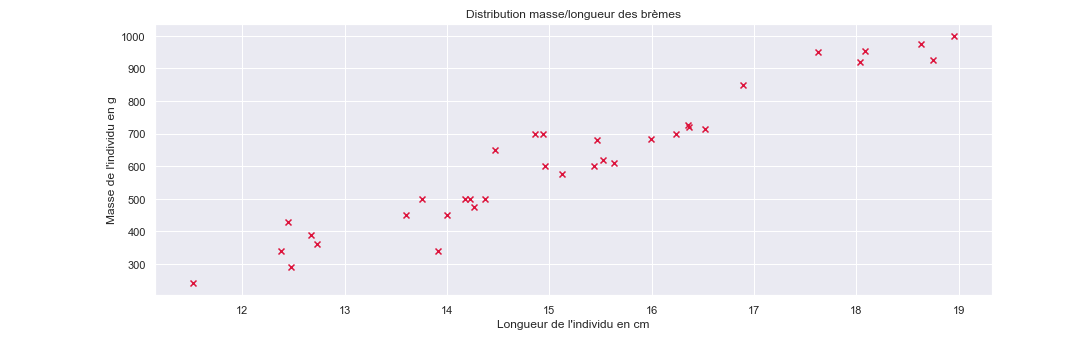
Ces points sont en grande partie issus de la branche du bas du graphe précédent ! Et une relation linéaire semblerait convenir. Nous avons donc eu raison (au moins pour cette espèce) de séparer les données. Se pourrait-il que le problème d'estimation soit résolu par une simple régression linéaire sur la longueur mesurée pour chacune des espèces ? Représentons les données masse/longueur mesurée en séparant chaque espèce :

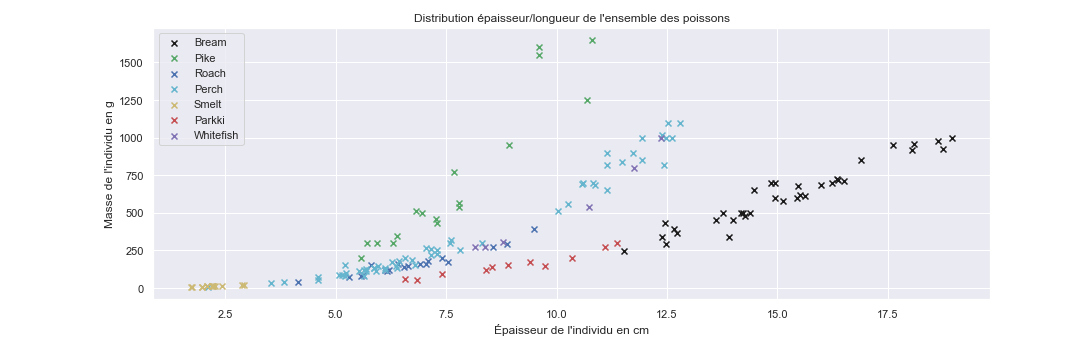
Et bien oui ! Ou plutôt, oui pour certaines espèces. Pour d'autres toutefois, il faudra utiliser un modèle plus complexe. Pour les "Pike" (brochets) par exemple, un modèle polynomial d'ordre 2 ou 3 pourrait mieux expliquer les données. Une bonne visualisation aura déjà, à ce stade, permis de résoudre une bonne partie du problème (alors que la distribution non-catégorisée par les espèces apparait complexe).
On observe également que les données ne sont pas équitablement réparties : certaines espèces (violet, jaune) sont sous-représentées quand d'autres (noir, vert) sont présentes en plus grande quantité. C'est un problème pour la robustesse des modèles catégoriques : difficile de se reposer sur un modèle avec 3 paramètres ou plus quand l'ensemble des données disponibles ne possède pas un cardinal significativement plus grand.
On peut enfin obtenir un graphe analogue pour la distribution masse/largeur :

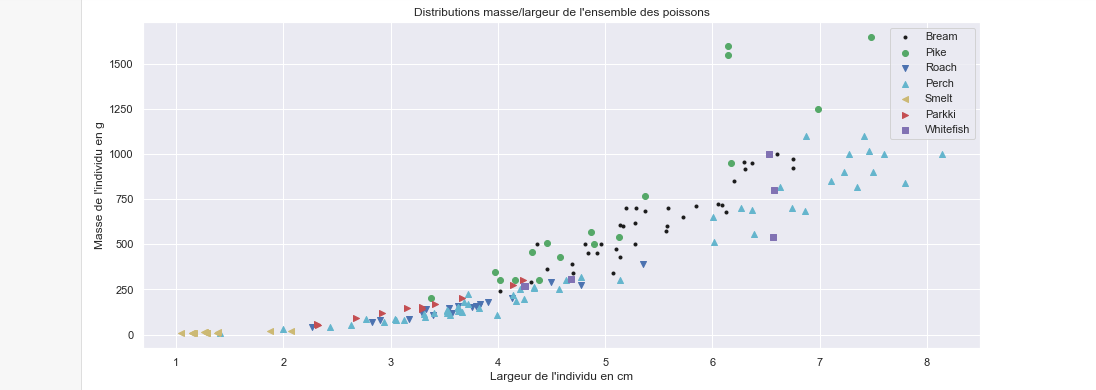
Les mêmes commentaires s'appliquent. Nous allons en effet voir maintenant que les features sont fortement corrélées et n'apportent pas d'informations supplémentaires entre elles. Pour cela, on utilise la matrice de corrélation des features, disponibles sous NumPy avec la méthode corr :

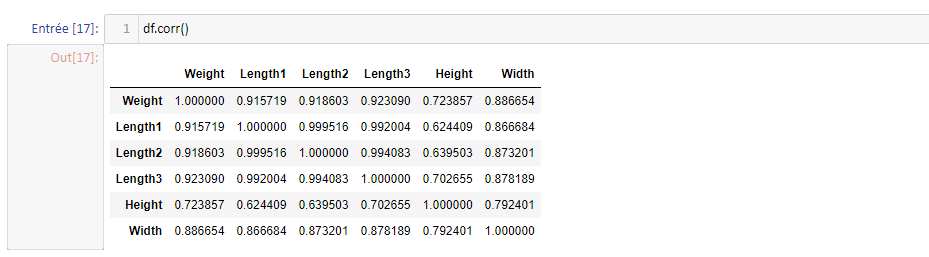
On remarque directement que toutes les variables explicatives sont fortement corrélées. "Length1" semble être la feature la plus corrélée avec la cible, on pourra ainsi l'utiliser préférentiellement pour le modèle de régression.
Pour conclure cet article, une autre méthode (moins explicite mais plus visuelle) de se représenter les liens entre variables homogènes comme ici (mais pas forcément les corrélations !) est de représenter la distribution des écarts absolus par paire de variables, comme proposé ici pour Length1 et 2 :

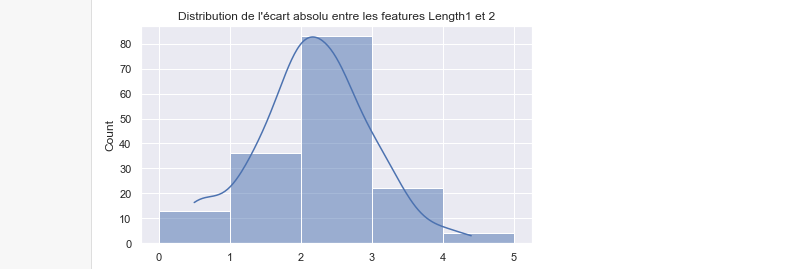
Notons enfin qu'il existe la fonction pairplot de Seaborn pour représenter les graphes de variations par paire (l'argument "kde" permet d'obtenir une densité plutôt qu'un histogramme sur la diagonale:



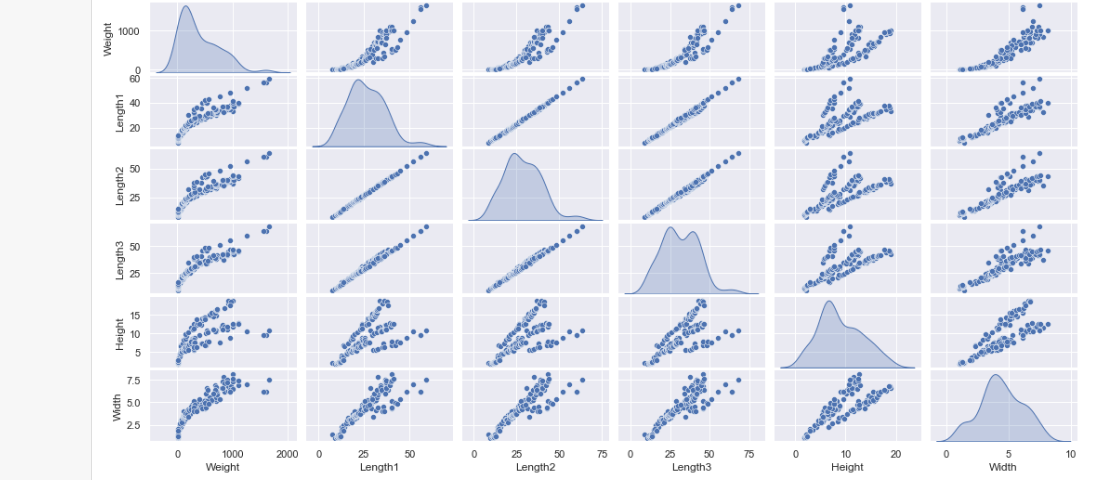
On note de belles corrélations linéaires ! Le dataset est artificiel, dans la pratique de tels résultats relèveraient du miracle.
Le prochain article traitera des modèles de régression (linéaire, polynomiale, multiple) appliqués sur ces données !